Для характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая (взвешенная), мода и медиана.

Расчет средней арифметической производится по сгруппированным данным, т.к некоторые значения признака повторяются.

Средняя арифметическая взвешенная определяется по формуле:

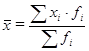; (2.1)

Мода - наиболее часто встречающееся значение признака.

В интервальном ряду определяется модальный интервал, т.е. интервал с наибольшим количеством повторений признака.

Значение моды определяется по формуле:

(2.2)

Медиана соответствует варианту, стоящему в середине ранжированного ряда.

Положение медианы определяется ее номером. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.

Численное значение медианы определяется по формуле:

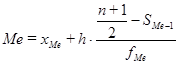; (2.3)

Прочее о социологии:

Дисфункции социального института
Нарушение нормативного взаимодействия с социальной средой, в качестве которой выступает общество или сообщество, называется дисфункцией социального института. Как отмечалось ранее, основой формирования и функционирования конкретного социа ...

Социальная общность и социальная группа. Социальные группы и их роль в общественной жизни
Группа - это такая совокупность людей, которые объединяются на основе совместной деятельности, общих целей. Она имеет свою систему жизненных ориентации, норм поведения, мораль, культуру и психологию, благодаря которым у индивида формируе ...

Программа «Молодежная практика»
В целях осуществления практических мер по решению проблем занятости и создания эффективной системы обучения молодежи непосредственно на рабочих местах с 1 января 1995 г. на территории Российской Федерации была введена в действие программа ...